![]()
Basic Law I: \GGjudge\GGconditional{\GGnonot a}{\GGconditional{b}{a}}![]()
Basic Law IIa: \GGjudge\GGconditional{\GGall{a}f(\mathfrak{a})}{\GGnoquant f(a)}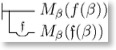
Basic Law IIb: \GGjudge\GGconditional{\GGall{f}M_{\beta}(\mathfrak{f}(\beta))}
{\GGnoquant M_{\beta}(f(\beta))}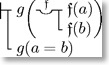
Basic Law III: \GGjudge\GGconditional{g(a=b)}{g\GGbracket{\GGall{f}\GGconditional
{\mathfrak{f}(b)}{\mathfrak{f}(a)}}}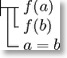
Basic Law IIIa: \GGjudge\GGconditional{\GGnonot g(a=b)}{\GGconditional{f(b)}{f(a)}}![]()
Basic Law IV: \GGjudge\GGconditional{\GGnot{(\GGcontent a)=(\kern4pt\GGnotalone b)}}
{\GGnonot{(\GGcontent a)=(\GGcontent b)}} ![]()
Basic Law V: \GGjudge(\spirituslenis{\varepsilon} f(\varepsilon)=\spirituslenis{\alpha} g(\alpha))=(\GGall{a}f(\mathfrak{a})=g(\mathfrak{a}))![]()
Basic Law Va: \GGjudge\GGconditional{\GGall{a}f(\mathfrak{a})=g(\mathfrak{a})}{\GGnoquant F(\spirituslenis{\varepsilon} f(\varepsilon))=F(\spirituslenis{\alpha}g(\alpha))}![]()
Basic Law Vb: \GGjudge\GGconditional{\spirituslenis{\varepsilon} f(\varepsilon)=\spirituslenis{\alpha}g(\alpha)}{f(a)=g(a)}![]()
Basic Law VI: \GGjudge a = \fgebackslash\spirituslenis{\varepsilon}(a=\varepsilon)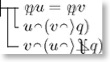
Proposition 32 ("right to left"-direction of Hume's Principle):
\GGjudge\GGconditional{\GGnonot v\fgecap(u\fgecap\rangle\fgeU q)}{\GGconditional{u\fgecap(v\fgecap\rangle q)}{\fgelb u=\fgelb v}}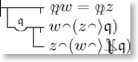
Proposition 49 (contrapositive of "left to right"-direction of Hume's Principle):
\GGjudge\GGconditional{\GGall{q}\GGconditional{\GGnonot z\fgecap(w \fgecap \rangle\fgeU \mathfrak{q})}{\GGnot w \fgecap(z \fgecap \rangle \mathfrak{q})}}{\GGnoquant\GGnonot\GGnot\fgelb w=\fgelb z}
Coming soon: Download the source code for Frege’s appendices to volume I (including table of basic laws, definitions, and important theorems) and volume II (including table of definitions and table of important theorems).